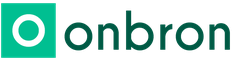График зависимости потенциальной энергии от расстояния. Потенциальная энергия взаимодействия молекул. Зависимость потенциальной энергии от расстояния между молекулами

При изучении поведения большой совокупности молекул вместо силы взаимодействия молекул удобнее пользоваться потенциальной энергией.

Нужно вычислять средние характеристики системы, а понятие средней силы взаимодействия молекул лишено смысла, так как сумма всех сил, действующих между молекулами, в соответствии с третьим законом Ньютона равна нулю. Средняя же потенциальная энергия в существенной мере определяет состояние и свойства вещества.

Зависимость потенциальной энергии от расстояния между молекулами

Так как изменение потенциальной энергии определяется работой силы, то по известной зависимости силы от расстояния можно найти зависимость от расстояния потенциальной энергии. Но нам достаточно знать лишь примерный вид потенциальной кривой Е р (r ). Прежде всего вспомним, что потенциальная энергия определяется с точностью до произвольной постоянной, потому что непосредственный смысл имеет не сама потенциальная энергия, а разность потенциальных энергий в двух точках, равная работе, взятой с противоположным знаком. Будем считать, как принято в физике, Е = 0 при r → ∞. Потенциальную энергию системы можно рассматривать как работу, которую система может совершить, причем потенциальная энергия определяется расположением тел, но не их скоростями. Чем больше расстояние между молекулами, тем большую работу совершат силы притяжения между ними при их сближении. Поэтому при уменьшении r , начиная от очень больших значений, потенциальная энергия будет уменьшаться. Мы приняли, что при r → ∞ потенциальная энергия равна нулю, следовательно, при уменьшении r потенциальная энергия становится отрицательной (рис. 2.12).

В точке r = r 0 сила равна нулю (см. рис. 2.10). Поэтому если молекулы расположены на этом расстоянии, то они будут покоиться, и никакую работу система совершать не может. Это означает, что при r = r 0 потенциальная энергия имеет минимум. Мы могли бы это значение потенциальной энергии Е p 0 принять за начало отсчета потенциальной энергии. Тогда она была бы всюду положительной (рис. 2.13). Обе кривые (см. рис. 2.12 и 2.13) одинаково характеризуют взаимодействие молекул. Разность значений Е р для двух точек одинакова у обеих кривых, а только она и имеет смысл.

При r < r 0 появляются быстро растущие силы отталкивания. Они также могут совершать работу. Поэтому потенциальная энергия при дальнейшем сближении молекул растет, причем очень быстро.

Потенциальная кривая будет иметь форму, изображенную на рисунке 2.12, если молекулы сближаются в плоскости А вдоль линии, соединяющей их центры (рис. 2.14). Если же молекулы сближаются в плоскости В или в плоскости С, то потенциальная кривая будет иметь вид, показанный соответственно на рисунках 2.15, а и 2.15, б.

Главная задача

Можно многое объяснить и понять, исходя из определенных представлений о характере взаимодействия молекул в веществе. Мы остановимся только на одном очень общем вопросе: каким образом знание зависимости потенциальной энергии от расстояния между молекулами позволяет установить количественный критерий различия между газами, жидкостями и твердыми телами с точки зрения молекулярно-кинетической теории.

Предварительно рассмотрим движение молекул с энергетической точки зрения.

Позволяет провести анализ общих закономерностей движения, если известна зависимость потенциальной энергии от координат. Рассмотрим для примера одномерное движение материальной точки (частицы), вдоль оси 0x в потенциальном поле, показанном на рис. 4.12.

Рис.4.12. Движение частицы вблизи положений устойчивого и неустойчивого равновесия

Поскольку в однородном поле сил тяжести потенциальная энергия пропорциональна высоте подъема тела, можно представить себе ледяную горку (пренебрегаем трением) с профилем, соответствующим функции П(x) на рисунке.

Из закона сохранения энергии E = К + П и из факта, что кинетическая энергия К = Е - П всегда неотрицательна, следует, что частица может находиться лишь в областях, где E > П . На рисунке частица с полной энергией E может двигаться только в областях

В первой области ее движение будет ограничено (финитно): при данном запасе полной энергии частица не может преодолеть «горок» на своем пути (их называют потенциальными барьерами ) и обречена вечно оставаться в «долине» между ними. Вечно - с точки зрения классической механики, которую мы сейчас изучаем. В конце курса мы увидим, как квантовая механика помогает частице выбраться из заточения в потенциальной яме - области

Во второй области движение частицы не ограничено (инфинитно), она может удалиться бесконечно далеко от начала координат направо, но слева ее движение по-прежнему ограничено потенциальным барьером:

Видео 4.6. Демонстрация финитного и инфинитного движений.

В точках экстремума потенциальной энергии x MIN и x MAX сила, действующая на частицу, равна нулю, потому что равна нулю производная потенциальной энергии:

Если поместить в эти точки покоящуюся частицу, то она оставалась бы там... опять-таки вечно, если бы не флуктуации ее положения. В этом мире нет ничего строго покоящегося, частица может испытывать небольшие отклонения (флуктуации ) от положения равновесия. При этом, естественно, возникают силы. Если они возвращают частицу к положению равновесия, то такое равновесие называется устойчивым . Если же при отклонении частицы возникающие силы еще дальше уводят ее от равновесного положения, то мы имеем дело с неустойчивым равновесием, и частица в таком положении обычно долго не задерживается. По аналогии с ледяной горкой можно догадаться, что устойчивым будет положение в минимуме потенциальной энергии, а неустойчивым - в максимуме.

Докажем, что это действительно так. Для частицы в точке экстремума x M (x MIN или x MAX ) действующая на нее сила F x (x M) = 0 . Пусть вследствие флуктуации координата частицы изменяется на небольшую величину x . При таком изменении координаты на частицу начнет действовать сила

(штрихом обозначена производная по координате x ). Учитывая, что F x =-П" , получаем для силы выражение

В точке минимума вторая производная потенциальной энергии положительна: U"(x MIN) > 0 . Тогда при положительных отклонениях от положения равновесия x > 0 возникающая сила отрицательна, а при x <0 сила положительна. В обоих случаях сила препятствует изменению координаты частицы, и положение равновесия в минимуме потенциальной энергии устойчиво.

Наоборот, в точке максимума вторая производная отрицательна: U"(x MAX)<0 . Тогда увеличение координаты частицы Δx приводит к возникновению положительной же силы, еще больше увеличивающей отклонение от положения равновесия. При x <0 сила отрицательна, то есть и в этом случае способствует дальнейшему отклонению частицы. Такое положение равновесия неустойчиво.

Таким образом, положение устойчивого равновесия может быть найдено при совместном решении уравнения и неравенства

Видео 4.7. Потенциальные ямы, потенциальные барьеры и равновесие: устойчивое и неустойчивое.

Пример . Потенциальная энергия двухатомной молекулы (например, Н 2 или О 2 ) описывается выражением вида

где r - расстояние между атомами, а A , B - положительные постоянные. Определить равновесное расстояние r М между атомами молекулы. Устойчива ли двухатомная молекула?

Решение . Первый член описывает отталкивание атомов на малых расстояниях (молекула сопротивляется сжатию), второй - притяжение на больших расстояниях (молекула сопротивляется разрыву). В соответствии со сказанным, равновесное расстояние находится при решении уравнения

Дифференцируя потенциальную энергию, получаем

Находим теперь вторую производную потенциальной энергии

и подставляем туда значение равновесного расстояния r M :

Положение равновесия устойчиво.

На рис. 4.13 представлен опыт по изучению потенциальных кривых и условий равновесия шарика. Если на модели потенциальной кривой поместить шарик на высоту большую высоты потенциального барьера (энергия шарика больше энергии барьера), то шарик преодолевает потенциальный барьер. Если начальная высота шарика меньше высоты барьера, то шарик остается в пределах потенциальной ямы.

Шарик, помещенный в наивысшую точку потенциального барьера, находится в неустойчивом равновесии, поскольку любое внешнее воздействие приводит к переходу шарика в нижнюю точку потенциальной ямы. В нижней точке потенциальной ямы шарик находится в устойчивом равновесии, поскольку любое внешнее воздействие приводит к возвращению шарика в нижнюю точку потенциальной ямы.

Рис. 4.13. Экспериментальное изучение потенциальных кривых

Дополнительная информация

http://vivovoco.rsl.ru/quantum/2001.01/KALEID.PDF – Приложение к журналу «Квант» - рассуждения об устойчивом и неустойчивом равновесии (А. Леонович);

http://mehanika.3dn.ru/load/24-1-0-3278 – Тарг С.М. Краткий курс теоретической механики, Изд,Высшая школа, 1986 г. – стр. 11–15, §2 – исходные положения статики.

Если в системе действуют только консервативные силы (потенциальное поле), то ее состояние можно охарактеризовать значением потенциальной энергии как функции координат.

Выберем какое-либо положение системы, которое условно примем за нулевое (положение 0), этому положению системы припишем потенциальную энергию По, равную нулю. Предположим теперь, что нам нужно определить потенциальную энергию системы в каком-то другом положении, которое назовем положением 1, т.е. величину П х. Потенциальной энергией системы в положении 1 называется величина, численно равная работе сил поля, которая совершается при переходе системы из данного положения в то, где потенциальная энергия выбрана равной нулю

Вследствие того, что поле потенциально, работа Л w не зависит от пути от 1 к 0, а характеризует систему в точке 1 по отношению к точке 0.

Если вслед за этим система перешла в положение 2, то ее потенциальная энергия стала П 2 , при этом по определению А 2[ - П 2 - Я,. Так как Л21 = -А 2 , работа

т.е. работа внутренних сил (сил поля) равна убыли потенциальной энергии. Наоборот, работа внешних сил, действующих против сил поля, приводит к приращению потенциальной энергии

Положение 0 было выбрано произвольно; за нулевое можно было бы выбрать любое другое положение и приписать ему значение П= 0. Это значит, что потенциальная энергия определяется с точностью до постоянного слагаемого константы С. Этот «произвол» не является практически существенным, так как при вычислении разности потенциальных энергий (см. например, выражения (1.123) - (1.125)) постоянные С в разности взаимно уничтожаются. Также не влияет присутствие постоянной С на производную от функции потенциальной энергии по координатам.

Полученные соотношения показывают, каким образом можно вычислить потенциальную энергию системы в определенном положении. Единой универсальной формулы (как это имеет место, например, для вычисления кинетической энергии) для этого нет. Соотношения (1.123) - (1.125) показывают путь (дают алгоритм или рецепт) определения потенциальной энергии системы посредством вычисления работы сил, приведших систему в данное положение.

В качестве примера разберем ряд важных случаев.

1. Вычислим потенциальную энергию упруго деформированной пружины. На рисунке 1.22, а приведена схема пружины в первоначально недеформи- рованном состоянии: левый конец пружины жестко закреплен, другой конец под действием внешней силы может перемещаться вдоль оси Ох. Изображена также растянутая под действием внешней силы пружина (см. рис. 1.22, б). В состоянии покоя на конец растянутой пружины вдоль оси х действуют две противоположно направленные силы: внешняя сила F 2 и сила упругости /), причем F[ = -F 2 . За нулевое положение (с нулевой потенциальной энергией) выбираем состояние недеформированной пружины (х = 0). В соответствии с (1.103) cL4 = - pxdx (Р - коэффициент жесткости) и

На графике (рис. 1.22, в) наклонная прямая линия выражает зависимость Е упр отх, а потенциальная энергия П(х) определяется затемненной площадью.

2. Второй пример связан с определением потенциальной энергии тела в гравитационном поле Земли. Обозначим массу Земли буквой М, а расстояние от центра Земли до тела массой т символом г. Тогда согласно закону всемирного тяготения (1.57)

За состояние с нулевой потенциальной энергией примем бесконечное удаление тела от Земли (/7(х) = 0). По определению потенциальную энергию тела в данной точке г гравитационного поля найдем как работу этой силы при перс-

п. , “гdr г Мт м

мещении тела из положения г в положение г -» » /7(г) = -GMm I - -G - .

После подстановки пределов получим r r r г

Величину ф = - называют потенциалом гравитационного поля. т

Потенциал гравитационного поля есть физическая величина, численно равная потенциальной энергии, которой обладает тело единичной массы, находящееся в данной точке поля. Потенциал гравитационного поля, создаваемого точечным телом (МТ) или однородным шаром, выражается формулой

Если известен потенциал поля в точке с координатой г, то потенциальная энергия тела определяется простым соотношением

3. Рассмотрим потенциальную энергию сжатого газа. Для этого представим себе цилиндр с поршнем, под которым находится газ. Подействуем внешней силой F на поршень. Под действием этой силы поршень, сжав газ, переместится на величину dx. Работу силы F над газом определим как cL4 = Fdx. Так как давление р = F/S, то F=pS и dA = pSdx, где Sdx =dV- величина изменения объема под цилиндром. Получили, что работа внешних сил dA равна увеличению потенциальной энергии газовой системы АП. То есть

Рассмотрим связь потенциальной энергии с силой. Так как потенциальная энергия и консервативные силы порознь являются функциями одних и тех же параметров (координат), между этими физическими величинами должна существовать связь. Установив эту связь, мы будем иметь возможность по заданной функциональной зависимости силы от координат точки поля (х, у, z), где эта сила F(x, у, z) действует, находить выражение для потенциальной энергии П(х, у, z) тела, нахолящегося в той же точке. Для установления этой связи рассмотрим тело в неизменном во времени (стационарном) поле. В каждой точке такого поля на тело будет действовать определенная сила F(x, у, z). В этой же точке поля тело будет иметь определенную (с точностью до константы Q потенциальную энергию П(х, у, z). Осуществим элементарное перемещение точки (тела) на величину d/. Внутренние силы поля в этом случае совершат работу -dll. Вследствие того, что по формуле (1.97) F/dl, изменение потенциальной энергии приравнивается работе dП = -F/dl, откуда

Проанализируем полученное выражение для трех случаев. Одномерное движение вдоль оси Ox: d/ =

Движение в центральном поле : d/ = dr

Общий трехмерный случай (в декартовых координатах):

т.е. сила равна взятому со знаком минус градиенту (антиградиенту) потенциальной энергии. Напомним, что градиентом является вектор, направление которого совпадает с направлением максимального возрастания скалярной функции (в нашем случае потенциальной энергии); его абсолютная величина определяет скорость возрастания функции в этом направлении (антиградиент имеет противоположное направление).

Как уже говорилось ранее, то, что потенциальная энергия определена с точностью до постоянного слагаемого, не влияет на результат вычислений по формулам (1.131) - (1.134). При дифференцировании это слагаемое не дает отличного от нуля вклада в выражение для силы.

Применим полученные соотношения для определения потенциальной энергии в уже известных нам случаях.

• 1. Потенциальная энергия упругой пружины. Так как F(x) = - (lx х х (F(x)) - упругая сила, ах - смещение конца положения равновесия, и так как F(x) = -(d/7/dx), то (1х = d/7(x)/dx, отсюда dП(х) = }